Artificial Neural Networks

18th November 2024

← By Rupok Ghosh

I am writing this as a review for my AI midterm where I am basically writing whatever I understood in the simplest language possible.

Artificial Neural Networks or ANNs are just copies of our own brain's neural networks but of course at a machine level with fewer capabilities ( humans on top! )

ANNs are nothing more than just a function, you take an input, let's say a handwritten number, process it in hidden layers and spit out the output, the value of the handwritten number.

Input -> Function -> Ouput

But of course, that's oversimplification by a stretch. Here's a drawing of a simple neural network:

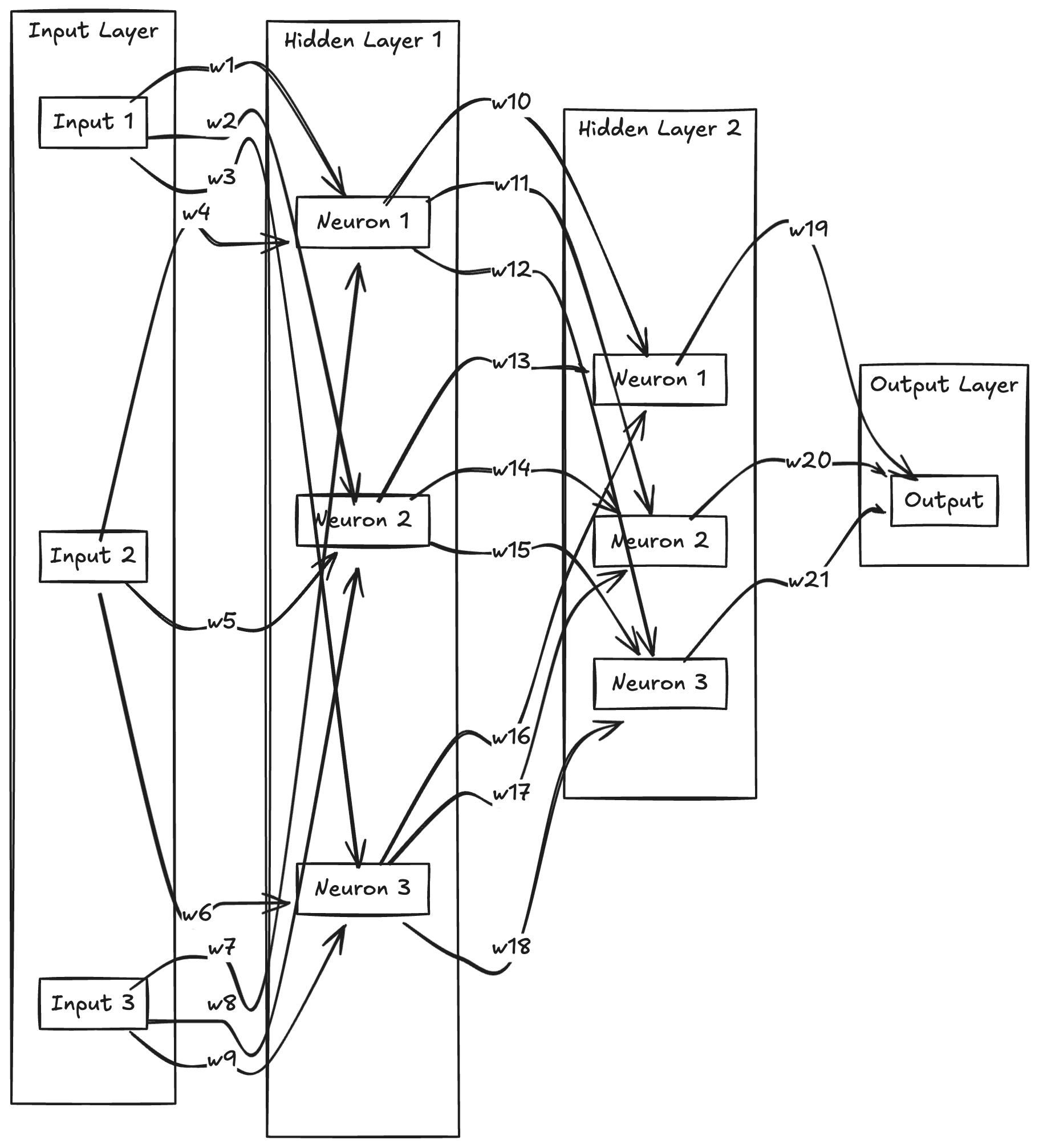
image of neural network

Think of an Artificial Neural Network (ANN) as three layers:

  1. Input Layer - Your data.
  2. Hidden Layers - Multiple layers where the data is processed (the bread and butter).
  3. Output Layer - The solution or basically whatever you want from your data.

The simplest version of an ANN would be a Perceptron which is a single-layer feed-forward network. It goes:

Input -> Weights -> Weighted Sum -> Step Function -> Output

Now you might be wondering what the hell are weights and step functions. Well let's dive deeper into proper neural networks and their functionalities.

Components of an ANN

  1. Neurons- basic units of computation, usually carries a number called activation between 0 and 1. Let's say we are trying to convert handwritten letters to numbers, each pixel will be a neuron with a number value corresponding to how bright that pixel is.

  2. Weights - defines the strength of connections between neurons. Basically the lines that connect neurons at each layer to the next one.

  3. Biases - we add it to the weighted sum of inputs to make calculations easier. It helps the model to adjust and shift activation thresholds.

  4. Activation function - the function that's used to calculate the activation ( the value/number ) of each neuron in the hidden layers. Some common activation functions are:

  1. Cost Function - a function that checks how terrible your output is, we use it to calculate how far "off" we are from the kind of solutions we expect from our neural network. We can then use that in Backpropagation to get better results by minimizing our cost function. (The higher the cost function, the more our solution is "off" our target )

  2. Back Propagation - Algorithm used to minimize error or the cost function by adjusting the weights and biases. We propagate back to our hidden layers and calculate how much each weight and bias contributed to the error using the chain rule of calculus. Then we determine how to adjust the weight and bias and use an optimization algorithm, such as gradient descent to do it. We repeat until the cost is minimized.

Issues with Backpropagation

Flow of Information

So how does the information flow?

Raw Data -> Input Layer ( neurons with values between 0 and 1 )

Input Layer -> Hidden Layers -> Next Layer -> .... -> Layer before Output Layer

This is where layers are connected with weights and then the activation of each neuron is calculated by feeding the sum of weights plus the bias to an activation function.

Hidden Layers -> Output Layer

Once we reach the output layer, we have our solution, then we compare the solution that our ANN gave us actual target values with which we calculate our cost function.

Hidden Layers <- Output Layer

Then we backpropagate to hidden layers to manipulate weights and biases that contribute to error and therefore, we reduce the error giving us better solutions after each run.

Repeat until desired or close to the desired solution.

Real World Applications of ANNs

Other stuff

Neural Evolutionary Models

HopField Networks

Neural Evolution